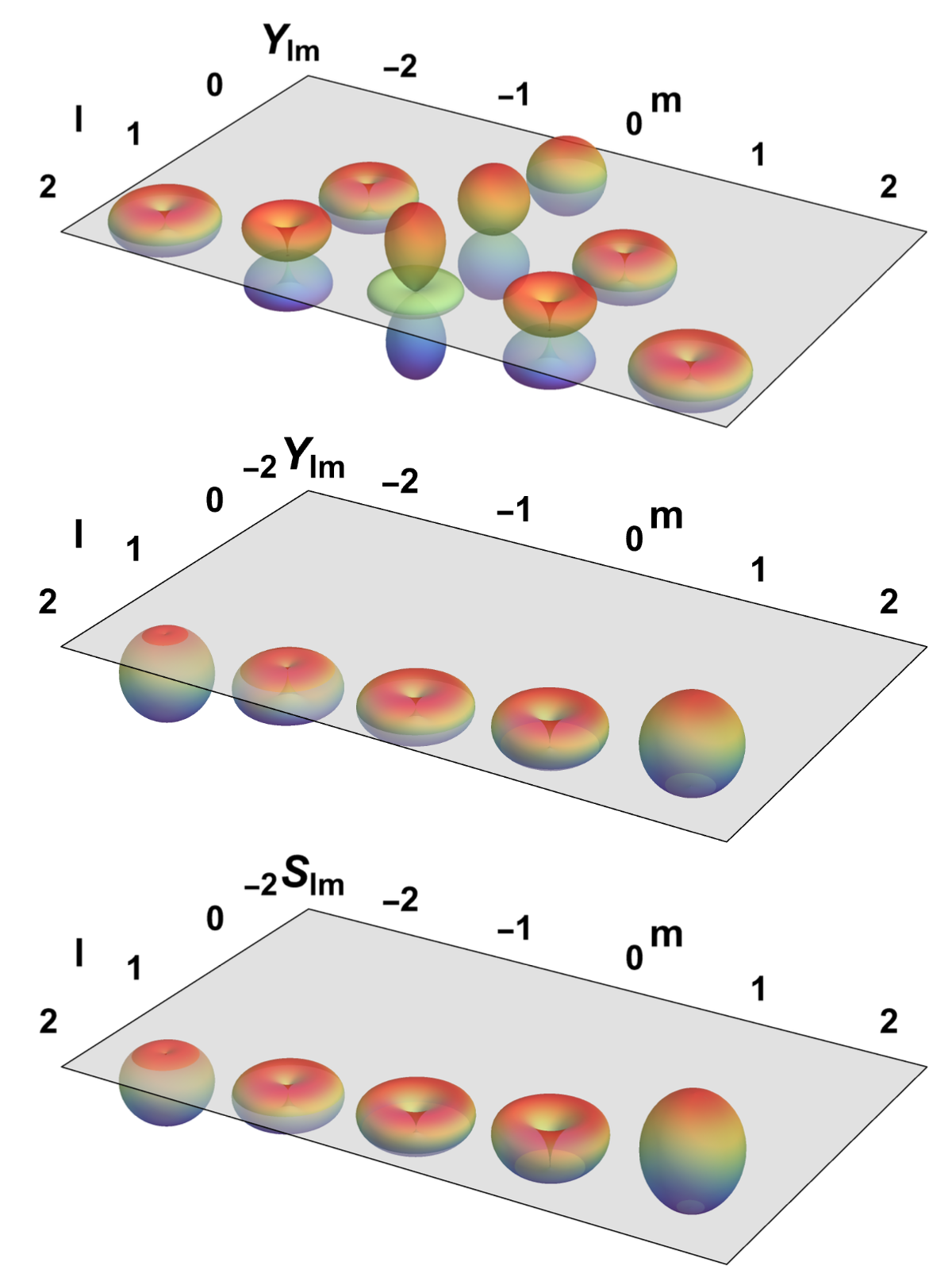
I have often wondered how the various spherical harmonic bases look in GR. In undergraduate classes you typically learn about the scalar spherical harmonics $Y_{\ell m}(\phi,\theta)$. The gravitational waves are typically described with the spin weighted spherical harmonics $Y_{\ell m}^{-2}(\phi,\theta)$. For example the complex time domain strain is

Finally, the spin-weighted spheroidal harmonics are the functions which are the eigenfunctions of the angular sector of the Teukolsky equation. These explicitly depend on $\omega$.

I find both the spin-weighted spherical/spheroidal harmonics buy using the black hole perturbation theory toolkit’s package SpinWeightedSpheroidalHarmonics.

Below, I make an image which shows how each of them look. I did this for spherocity parameter $\gamma = \omega \chi \sim 0.7$. You can see that the spheroidal harmonics have preferential radiation in the upward direction comparing $m=-2$ vs $m=2$. This is because the retrograde mode is weaker, and has a different QNM frequency than the prograde one (slower frequency and similar damping rate).

You can view the slides here directly.

Natural units are a way to simplify repetitive fundamental constants in theoretical physics equations. In my research, I used three particular unit systems: geometric ($c=G=1$), natural ($c=\hbar=1$), and Planck units ($c=\hbar=G=1$). However, for me it is time consuming to convert to and from natural units. I decided that I would write an extension to Mathematica’s units package to remedy this.

A great summary of natural units goes in more detail in an excellent document here. Given a SI quantity $Q_{\text{SI}}$, the quantity in natural units is given by $Q_{\text{geometric}} = Q_{\text{SI}}/A$ for some factor $A$. For the rest of this post, I will use geometric units. Suppose that the quantity has SI units of the form

then, one can find $Q_{\text{geometric}}$ with the following factor

So all we need to do to convert between the units is to find $A$.

Mathmatica Implementation

The first thing that we need to do is write a helper function that will return the $\alpha$, $\beta$, and $\gamma$ from our previous equation. All I need to do was write a wrapper class for the UnitDimensions[] fuction that Mathematica has.

GetUnitVal[qu_, unit_] := Module[{result, dims},
  dims = UnitDimensions[qu];
  If[Position[dims, unit] == {}, result = 0,
    result = dims[[Position[dims, unit][[1, 1]], 2]]];
  result
]

Next, I wrote a function to calculate the constant $A$.

SItoGeometricDivideFactor[qu_] := Module[{\[Alpha], \[Beta], \[Gamma]},
  \[Alpha] = GetUnitVal[qu, "MassUnit"]; \[Beta] =
   GetUnitVal[qu, "LengthUnit"]; \[Gamma] = GetUnitVal[qu, "TimeUnit"];
   Quantity[1, "GravitationalConstant"]^-\[Alpha]*
   Quantity[1, "SpeedOfLight"]^(2 \[Alpha] - \[Gamma])
]

Finally, I used a function that will find $Q_{\text{geometric}}$ by dividing $Q_{\text{SI}}$ by $A$. Afterwards, it converts the result into meters to the $n$ power as is used in geometric units.

SItoGeometricUnits[qu_] := Module[{factor, geoqu},
  factor = SItoGeometricDivideFactor[qu]; geoqu = qu/factor;
   UnitConvert[geoqu, ("Meters")^GetUnitVal[geoqu, "LengthUnit"]]
]

The full version of these functions which includes geometric, natural, and Planck units is publicly available on my Github. Feel free to use it and I hope that it will save you time in your research!

You can view the slides here directly.

You can view the slides here directly.

You can view the slides here directly.

You can view the poster here directly.

You can view the paper at 1808.00080.

The abstract is as follows:

Binary pulsars allow us to carry out precision tests of gravity and have placed stringent bounds on a broad class of theories beyond general relativity. Current and future radio telescopes, such as FAST, SKA, and MeerKAT, may find a new astrophysical system, a pulsar orbiting around a black hole, which will provide us a new source for probing gravity. In this paper, we systematically study the prospects of testing general relativity with such black hole-pulsar binaries. We begin by finding a mapping between generic non-Einsteinian parameters in the orbital decay rate and theoretical constants in various modified theories of gravity and then summarize this mapping with a ready-to-use list. Theories we study here include scalar-tensor theories, varying G theories, massive gravity theories, generic screening gravity and quadratic curvature-corrected theories. We next use simulated measurement accuracy of the orbital decay rate for black hole-pulsar binaries with FAST/SKA and derive projected upper bounds on the above generic non-Einsteinian parameters. We find that such bounds from black hole-pulsars can be stronger than those from neutron star-pulsar and neutron star-white dwarf binaries by a few orders of magnitude when the correction enters at negative post-Newtonian orders. By mapping such bounds on generic parameters to those on various modified theories of gravity, we find that one can constrain the amount of time variation in Newton’s constant G to be comparable to or slightly weaker than than the current strongest bound from solar system experiments, though the former bounds are complementary to the latter since they probe different regime of gravity. We also study how well one can probe quadratic gravity from black hole quadrupole moment measurements of black hole-pulsars. We find that bounds on the parity-violating sector of quadratic gravity can be stronger than current bounds by six orders of magnitude. These results suggest that a new discovery of black hole-pulsars in the future will provide powerful ways to probe gravity further.

You can view the final report here directly.

Alternatively, the full directory containing my work that summer can be found here.

You can view the final report here directly.

Alternatively, the full directory containing my work that summer can be found here.